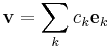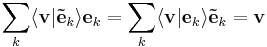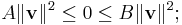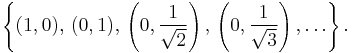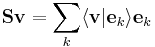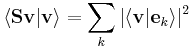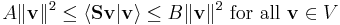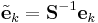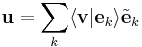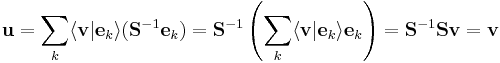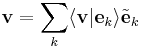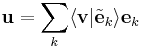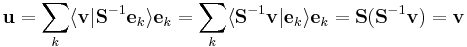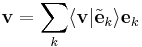Frame of a vector space
In linear algebra, a frame of a vector space V with an inner product can be seen as a generalization of the idea of a basis to sets which may be linearly dependent. The key issue related to the construction of a frame appears when we have a sequence of vectors  , with each
, with each  and we want to express an arbitrary element
and we want to express an arbitrary element 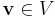 as a linear combination of the vectors
as a linear combination of the vectors 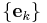 :
:
and want to determine the coefficients 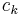 . If the set
. If the set 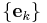 does not span
does not span  , then these coefficients cannot be determined for all such
, then these coefficients cannot be determined for all such 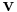 . If
. If 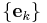 spans
spans  and also is linearly independent, this set forms a basis of
and also is linearly independent, this set forms a basis of  , and the coefficients
, and the coefficients 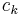 are uniquely determined by
are uniquely determined by 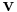 : they are the coordinates of
: they are the coordinates of 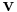 relative to this basis. If, however,
relative to this basis. If, however, 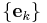 spans
spans  but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if
but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if  is of infinite dimension.
is of infinite dimension.
Given that 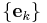 spans
spans  and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:
and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:
- By removing vectors randomly from the set, it may lose its possibility to span
 before it becomes linearly independent.
before it becomes linearly independent. - Even if it is possible to devise a specific way to remove vectors from the set until it becomes a basis, this approach may become infeasible in practice if the set is large or infinite.
- In some applications, it may be an advantage to use more vectors than necessary to represent
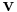 . This means that we want to find the coefficients
. This means that we want to find the coefficients 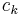 without removing elements in
without removing elements in 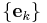 .
.
In 1952, Duffin and Schaeffer gave a solution to this problem, by describing a condition on the set 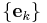 that makes it possible to compute the coefficients
that makes it possible to compute the coefficients 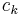 in a simple way. More precisely, a frame is a set
in a simple way. More precisely, a frame is a set 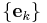 of elements of V which satisfy the so-called frame condition:
of elements of V which satisfy the so-called frame condition:
- There exist two real numbers, A and B such that
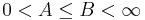 and
and
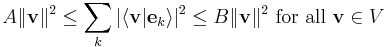 .
.
- This means that the constants A and B can be chosen independently of v: they only depend on the set
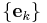 .
.
The numbers A and B are called lower and upper frame bounds.
It can be shown that the frame condition is sufficient to be able to find a set of dual frame vectors 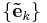 with the property that
with the property that
for any 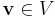 . This implies that a frame together with its dual frame has the same property as a basis and its dual basis in terms of reconstructing a vector from scalar products.
. This implies that a frame together with its dual frame has the same property as a basis and its dual basis in terms of reconstructing a vector from scalar products.
Contents |
Relation to bases
If the set 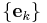 is a frame of V, it spans V. Otherwise there would exist at least one non-zero
is a frame of V, it spans V. Otherwise there would exist at least one non-zero 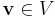 which would be orthogonal to all
which would be orthogonal to all 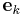 . If we insert
. If we insert 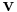 into the frame condition, we obtain
into the frame condition, we obtain
therefore 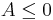 , which is a violation of the initial assumptions on the lower frame bound.
, which is a violation of the initial assumptions on the lower frame bound.
If a set of vectors spans V, this is not a sufficient condition for calling the set a frame. As an example, consider 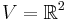 and the infinite set
and the infinite set 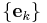 given by
given by
This set spans V but since 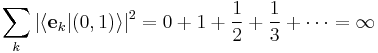 we cannot choose
we cannot choose 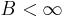 . Consequently, the set
. Consequently, the set 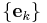 is not a frame.
is not a frame.
Types of frames
Tight frames
A frame is tight if the frame bounds  and
and  are equal. This means that the frame obeys a generalized Parseval's identity. For example, the union of
are equal. This means that the frame obeys a generalized Parseval's identity. For example, the union of  orthonormal bases of a vector space forms a tight frame with
orthonormal bases of a vector space forms a tight frame with 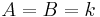 . If
. If 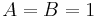 , then a frame is either called normalized or Parseval. However, some of the literature refers to a frame for which
, then a frame is either called normalized or Parseval. However, some of the literature refers to a frame for which 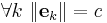 where
where  is a constant independent of
is a constant independent of  (see uniform below) as a normalized frame.
(see uniform below) as a normalized frame.
Uniform frames
A frame is uniform if each element has the same norm: 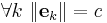 where
where  is a constant independent of
is a constant independent of  . A uniform normalized tight frame with
. A uniform normalized tight frame with 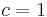 is an orthonormal basis.
is an orthonormal basis.
The dual frame
The frame condition is both sufficient and necessary for allowing the construction of a dual or conjugate frame, 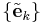 , relative the original frame,
, relative the original frame, 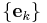 . The duality of this frame implies that
. The duality of this frame implies that
is satisfied for all 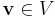 . In order to construct the dual frame, we first need the linear mapping:
. In order to construct the dual frame, we first need the linear mapping: 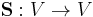 defined as
defined as
From this definition of 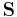 and linearity in the first argument of the inner product, it now follows that
and linearity in the first argument of the inner product, it now follows that
which can be inserted into the frame condition to get
The properties of 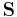 can be summarised as follows:
can be summarised as follows:
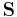 is self-adjoint, positive definite, and has positive upper and lower bounds. This leads to
is self-adjoint, positive definite, and has positive upper and lower bounds. This leads to- the inverse
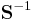 of
of 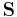 exists and it, too, is self-adjoint, positive definite, and has positive upper and lower bounds.
exists and it, too, is self-adjoint, positive definite, and has positive upper and lower bounds.
The dual frame is defined by mapping each element of the frame with 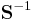 :
:
To see that this make sense, let 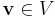 be arbitrary and set
be arbitrary and set
It is then the case that
which proves that
Alternatively, we can set
By inserting the above definition of 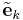 and applying known properties of
and applying known properties of  and its inverse, we get
and its inverse, we get
which shows that
This derivation of the dual frame is a summary of section 3 in the article by Duffin and Schaeffer. They use the term conjugate frame for what here is called dual frame.
History
Frames were introduced by Duffin and Schaeffer in their study on nonharmonic Fourier series. They remained obscure until Mallat, Daubechies, and others used them to analyze wavelets in the 1980s. Some practical uses of frames today include robust coding and design and analysis of filter banks.
See also
References
- Ole Christensen (2003). An Introduction to Frames and Riesz Bases. Birkhäuser.
- R. J. Duffin and A. C. Schaeffer (1952). "A class of nonharmonic Fourier series". Trans. Amer. Math. Soc. (Transactions of the American Mathematical Society, Vol. 72, No. 2) 72 (2): 341–366. doi:10.2307/1990760. JSTOR 1990760.
- Jelena Kovacevic, Pier Luigi Dragotti, and Vivek Goyal (June 2002). "Filter Bank Frame Expansions with Erasures". IEEE Trans. Information Theory 48 (6): 1439–1450. doi:10.1109/TIT.2002.1003832. http://citeseer.ist.psu.edu/cache/papers/cs/28168/http:zSzzSzlcavwww.epfl.chzSz~dragottizSzpublicationszSzIT_june02.pdf/kovacevic02filter.pdf.